简单聊聊因果推断这个事。
Thoughtworks 曾与一家国际知名药企合作,解决患者用药依从性低(从药物治疗的角度,药物依从性是指患 者对药物治疗方案的执行程度)的问题。
如果仅着眼于患者本身,其不持续用药,也许是忘了,或者动力不足,看似可以简单归因并立刻着手解决。但 当我们打开这个问题,置身于整个系统,会发现影响患者持续用药的因素涉及方方面面。
除患者个人层面,涉及到的利益相关方包含患者、医院、医生、制药机构、医药代理、甚至政府机构。其中影 响因素可能有医生对患者的影响、医疗保险的报销规定、社区医疗资源分布、甚至家人的陪伴等等。多层因素 之间亦互相牵连,相互影响。
最终发现,从患者主观能动性出发所能提升的用药依从性大概只占小部分。而医生对患者的支持,以及医保的 报销比例,或许更大程度决定了患者是否持续用药。
一个原本以为从患者角度的动机或者习惯问题,在深入研讨后会发现它是一个更大的系统问题,而非个人动机的问题。
这正是我们今天的现状,我们所面临的大部分问题是一团缠绕的纱线。因此,为了避免想当然从某个点随意牵 扯一条线而造成“死结”,我们需要花更多的时间与精力,来解开这团纱线。
D o n e l l a M e a d o w s 在 《 系 统 之 美 》中提到:“厘清影响问题的各个元素并理解其间的关系 , 我们才能更好找出所谓问题的杠杆解。” 。我们在解决问题时需要关注问题所处的上下文、系统关系,以及各个元素之间的内部因果与联系。复杂问题之间互为因果、环环嵌套,因而有时难以分析和筛选、聚焦于某个单一问题而创造的方案,往往只是局部优化。为此我们需要分析每个问题的产生原因和影响结果,找到某个问题所关联的上下游问题。
贝叶斯提出的逆概率定理,认为概率现象也是主观信念程度的变化和更新,让概率也失去了客观性;统计学创始人高尔顿和学生皮尔逊用相关关系取代了因果关系。至此,基于统计的科学研究壮大发展,因果效应基于统计计量的研究开启。
计量经济学家格兰杰基于概率形式给出因果检测公式,论证事件发生是否存在先后的显著性。但是只能判断发生事件在时间上的先后是否有统计显著性,并不能判断因果。
但相关性并不能准确的说明因果关系。相关性并不能取代因果性,无法处理具有共同混杂因子的变量关系,统计数据常因果颠倒(无方向性)、造就伪相关、对数据要求也很高(iid)、泛化性、鲁棒性都很差。
那么如何分析因果关系以及将其用在实践中就需要借助一些更高效的工具和手段。
我们首先来定义下什么是因果,休谟在《人类理解研究》中提到:“我们可以给一个因下定义说,它是先行于、接近于另一个对象的一个对象,而且在这里,凡与前一个对象类似的一切对象都和与后的一个对象类似的那些对象处在类似的先行关系或者接近关系中。或者,换言之,假如没有前一个对象,那么后一个对象就不可能存在。”(最后那句话也是反事实的定义。)
在图灵奖得主朱迪尔·珀尔(Pearl)在 2000 年的论文《 Causality: Models, Reasoning, and inference》中提出了因果阶梯论(Pearl Causal Hierarchy):
他认为,因果推断有三个层级,
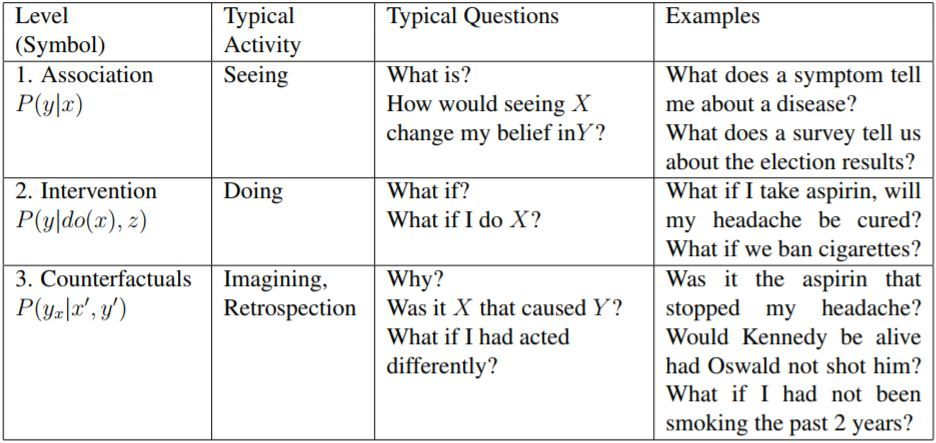
最低的第一层级是相关(association),涉及的是预测,而不涉及因果关系,只讨论变量之间的关联,比如公鸡打鸣与日出之间的相关关系。
第二层级是干预(intervention),涉及因果性,比如吸烟与患肺癌之间的因果关系。
第三层级是反事实(Counterfactuals),涉及的是回答诸如“如果情况不是现在这样,可能会发生什么”的问题。
在论文中也提到了我们常遇到的五个问题:
- 给定的疗法在治疗某种疾病上的有效性?
- 是新的税收优惠导致了销量上升吗?
- 每年的医疗费用上升是由于肥胖症人数的增多吗?
- 招聘记录可以证明雇主的性别歧视罪吗?
- 我应该放弃我的工作吗?
我们常说相关性不等于因果性,但这些问题的一般特征是它们关心的都是什么东西带来的效果,但我们并没有很好的办法和科学的办法能够表达这样的问题,以及确保我们的结论不出问题。现实世界中绝大多数东西我们都很难找到准确因和果,往往都是复杂的、环环相扣的、互相影响的。
耶日• 内曼在 1923 年发表了《On the Applications of the Theory of Probability to Agricultural Experiments》他提出了用于因果推断的“潜在结果”(potential outcomes)的数学模型,并将它和统计推断结合起来。
一个或多个处理作用在个体上产生的预期效果我们称之为潜在结果 (Potential outcome)。之所以称为潜在结果是因为在一个个体上最终只有一个结果会出现并被观察到,也就是和个体所接受的处理相对应的那个结果。另外的潜在结果是观察不到的,因为它们所对应的处理并没有实际作用在该个体上。因果效果的定义依赖于潜在结果,但是它并不依赖于哪一个潜在结果实际发生。
Rubin(1974)重新独立地提出了潜在结果的概念,提出了鲁宾因果模型,将潜在结果框架扩展为在观察性和实验性研究中思考因果关系的一般框架。
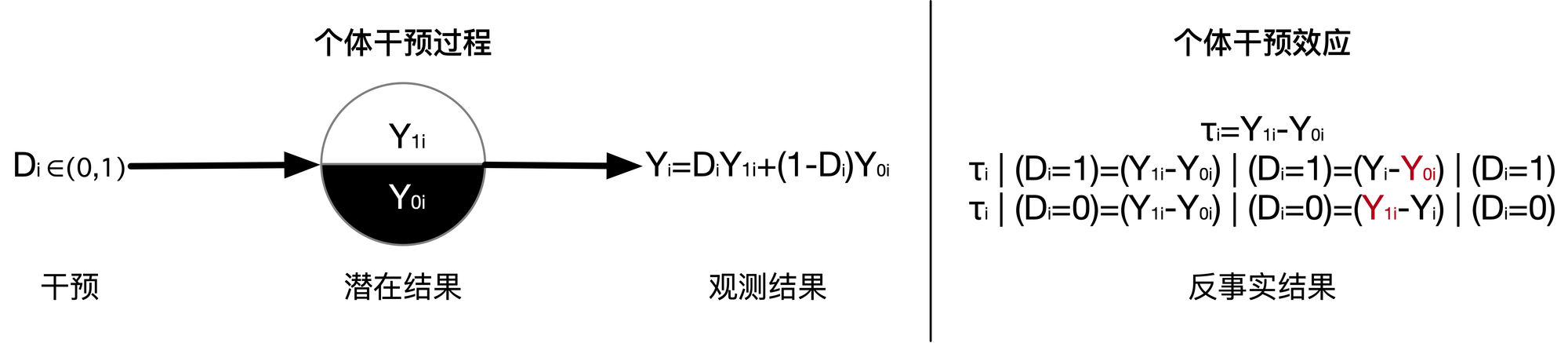
鲁宾因果模型是基于潜在结果的想法。例如,如果一个人上过大学,他在 40 岁时会有特定的收入,而如果他没有上过大学,他在 40 岁时会有不同的收入。为了衡量这个人上大学的因果效应,我们需要比较同一个人在两种不同的未来中的结果。由于不可能同时看到两种潜在结果,因此总是缺少其中一种潜在结果。这种困境就是“因果推理的基本问题”。
由于因果推理的根本问题,无法直接观察到单元级别的因果效应。然而,随机实验允许估计人口水平的因果效应。随机实验将人们随机分配到对照组:大学或非大学。由于这种随机分配,各组(平均)相等,40 岁时的收入差异可归因于大学分配,因为这是各组之间的唯一差异。然后可以通过计算处理(上大学)和对照(非上大学)样本之间的平均值差异来获得平均因果效应(也称为平均处理效应)的估计值。
然而,在许多情况下,由于伦理或实际问题,随机实验是不可能的。在这种情况下,存在非随机分配机制。上大学的例子就是这种情况:人们不是随机分配上大学的。相反,人们可能会根据他们的经济状况、父母的教育等来选择上大学。已经开发了许多用于因果推断的统计方法,例如倾向得分匹配。这些方法试图通过寻找类似于处理单元的控制单元来纠正分配机制。
Pearl 和 Mackenzie 在《The Causal Revolution》中提出了一种因果结构模型——SCM。SCM 由三部分构成:
- 图模型(Graphical models)
- 结构化方程(Structural equations)
- 反事实和介入式逻辑(Counterfactual and interventional logic)
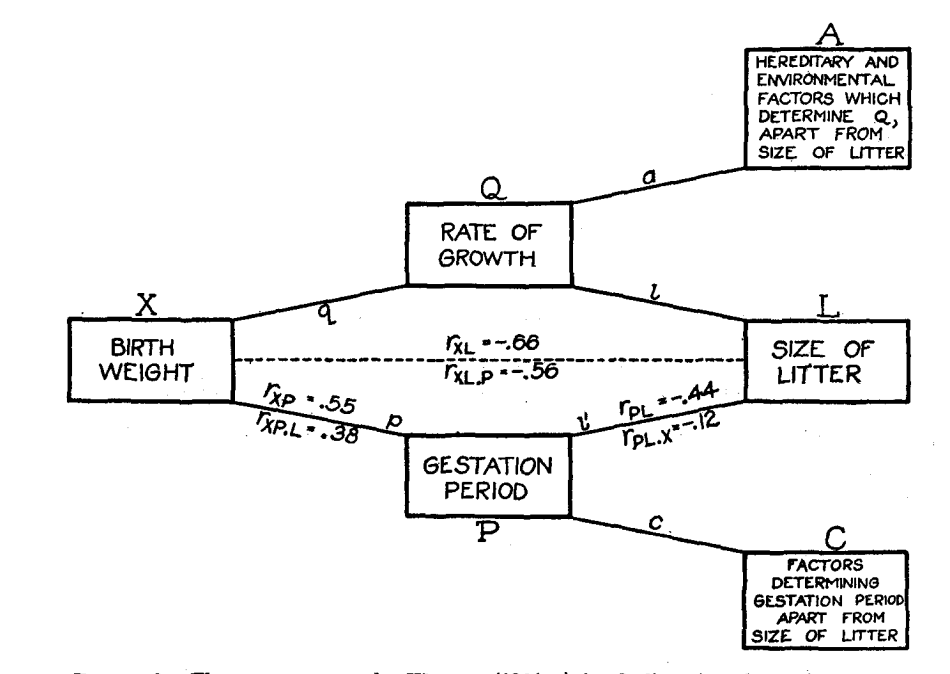
图模型最早是由 遗传学家 Sewell Wright 在 1918 年左右提出的,最初是为了推断决定豚鼠出生体重的因素的相对重要性。他利用这种结构发展了路径分析的方法,这种技术通常用于分层和复杂过程的因果推断任务,如表型遗传。
他在 1921年的论文《Correlation and Causation》就有画因果图,描述各种遗传因素与豚鼠出生体重之间关系的结构性因果模型的代表。Wright的路径追踪规则定义了一套使用一组关联关系的规则,以生成一个因果图。因果图也可以被认为是结构因果模型的 DAG 表示方法。
抽烟的人容易导致肺癌,抽烟的人也容易出现黄手指。因为抽烟这个“共因”,“黄手指”和“肺癌”产生了关联,我们不难发现,手指黄的人很多都容易患肺癌。但是我们不能说,黄手指会导致肺癌,它俩并没有因果关系。这个“共因”也被称之为“混杂因子”(confounder)。在这个例子中,“抽烟”就是“黄手指”和“肺癌”的混杂因子,它让“黄手指”和“肺癌”出现了一种“伪相关”,这种伪相关也被称为“偏倚”(bias)。,因果推理的一大目标就是尽量消除混杂带来的偏倚(也就是那些非因果的关联关系),找出真正的因果关系。
在因果关联领域有一个著名的法则,被称为d-分离法则。d-分离的全称是有向分离(directional separation),是一种判断变量是否条件独立的方法。
我们可以通过后门准则来消除混杂因子的影响。如果我们有足够的数据能够将所有A和 Y 之间的后门路径全部阻断,那么我们就可以识别(identify)A和 Y 之间的因果关系。
简单来说,混杂(confounding)就是因果变量之间的共因。而混杂因子(confounder)就是能够阻断因果变量之间所有后门路径的变量(可能混杂因子不止一个)。这里要特别说明的是,混杂因子的概念是建立在因果图结构之上的,必须要指定因果图的结构,混杂因子才有意义。在一个复杂的因果图中,某个变量可能阻断了某两个变量之间的所有后门路径,因此它是某两个变量的混杂因子,但它对另一个路径来说可能并不是混杂因子。因此我们纠缠于谁是混杂因子没有实际意义,有意义的是,以哪个变量为条件可以消除这条路径上的混杂。
让我们回到现实的场景中。
传统的机器学习是预测工作,拟合用户的特征和目标 Y 值之间的关系,但无法建模实验前后对业务目标带来的收益。而因果推断可以拆分实验变量 T 和协变量 X(用户特征),来构建不同用户在不同实验下产生的不同行为的因果模型。
我们可以通过公式看看。下面是一个经典的贝叶斯公式:
$$P(Y \mid X)=\frac{P(X, Y)}{P(X)}=\frac{P(X \mid Y) P(Y)}{P(X)} \quad P\left(X_{k} \mid Y=1\right)=\frac{P\left(X_{k}\right) P\left(Y=1 \mid X_{k}\right)}{P(Y=1)}$$
当已知结果发生了(Y=1),相分析引起结果的原因 \(X_k\)。通过贝叶斯公式发现 \(P(X_k)\) 也就是 \(X_k\)的概率越高,\(Y\) 的概率越高,但这个概率高低是非因果的。
下面是 SCM 因果推断的公式:
$$P(Y \mid d o(X))=\sum_{u} P(Y \mid X, u) P(u)$$
我们可以发现在控制了 u 的情况下,切断了 u -> x 的后门路径,那就可以通过干预某些有意义的变量来评估因果效应。现实中常见的场景是在有某些约束的情况下,如何给目标客户分配合适的权益,从而达到业务目标最大化。
我们可以假设我们是一个电商网站,我们需要通过优惠券刺激用户消费。那么在总成本不变下发什么样的折扣券给到什么样的用户效果最好呢?
我们可以将不同的用户进行划分,然后对不同用户群体做 AB Test 发放不同的优惠券,从而来观测哪些用户群体的适合哪些优惠券,效果更加好。只预测收到优惠券后产生的借款。无法区别对活动更敏感人群和自然转化人群。但通过Uplift 的增量进行建模,即优惠券而产生的收益,就能够精准找到对活动更敏感人群。
Uplift models 用于预测一个 treatment 的增量反馈价值。举个例子来说,假如我们想知道对一个用户展现一个广告的价值,通常的模型只能告诉我们用户在展示广告后的购买意愿很强,但事实很有可能是他们在被展示广告之前就已经很想购买了。Uplift models 聚焦于用户被展示广告后购买意愿的增量。
在一个理想的世界中我们能够将每一个个体根据类型划分,然后找到 “persuadables” 的那一波人,也就是投资汇报率最高的那一波人。对于 “sleeping dogs” 的那一波人肯定不是营销的目标人群。但是在现实生活中我们却没有办法准确的判断一个人是属于哪种类型,因为我们不可能对同一个用户 treated 或者 notreated。但是借助统计和机器学习的知识,我们就可以得到相似的用户大致会怎么反应。这就是 uplift 模型的核心,每一个用户会得到一个位于 -1 到 1 的 lift score,用于指导用户人群的选择。
用 uplift 模型可以辅助你找到更合适的用户进行实验。而在推荐上的具体工作像是《Causal intervention for leveraging popularity bias in recommendation》这篇论文也详解得很好,里面详细分析了分析如何使用因果推断来消除流行度偏差。
总结一下,因果推断非常适合解决某个场景下选择某一批用户用某个手段得到某个收益的互联网场景,但这个领域在 AI 和互联网具体场景下还是很原始,有待发展。还有像因果发现、因果强化学习、因果推断、与深度学习结合等等子方向还在蓬勃发展中。个人来说还是很相信因果推断会是个大势,可能将来会大量与机器学习、深度学习融合。在现实中干预一个目标的已知因子、混杂因子是非常非常多的,如何找到合适的因子也会成为一个大难题。




