极大极小
极大极小算法常用于二人博弈游戏,目的是寻找最优的方案使得自己能够利益最大化。
如下图(图中用到了剪枝,这个下面再讲),A和B博弈,假设A和B都足够聪明,会选择当前利益最大化的步子。A为了最大利益,选择最大值,B为了使A最小利益,选择最小值。
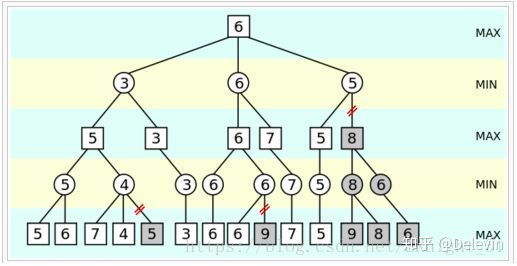
选择值的过程如下:
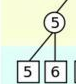
从下往上填值,左下角有如下图节点,在5、6中选择最小值,因此选到了5。
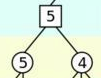
然后再继续到上一层,如下图,5、4中选择最大值,选中了5。
按照这个选择方式,填满了树。
Alpha-Beta 剪枝算法
剪枝是希望在搜索的时候,根据已搜索的结果,剔除超出最优解的分支,那么意味着这个分支下的所有节点都不需要考虑了,大大降低了搜索的次数。
对于每个节点值n,假设α为下界,β为上界,对于α ≤ n ≤ β:
若 α ≤ β 则n有解。
若 α > β 则n无解。
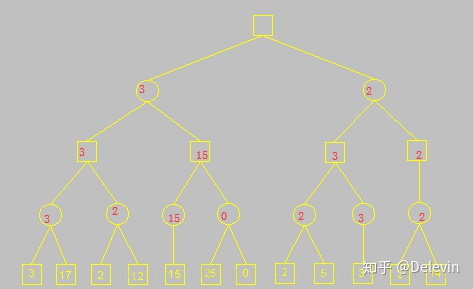
从左下角开始,节点选出最小值3
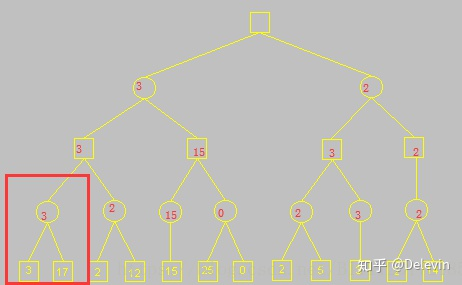
然后继续往上,取了3,那么得出如下结果:
B节点 上限β = 3 ,下限α = 负无穷。
A节点 上限β = 无穷 ,下限α = 3。
推到出C节点 上限β = 2 ,下限α = 3。
由于α > β,而C节点的12应该被剪枝,如下图:
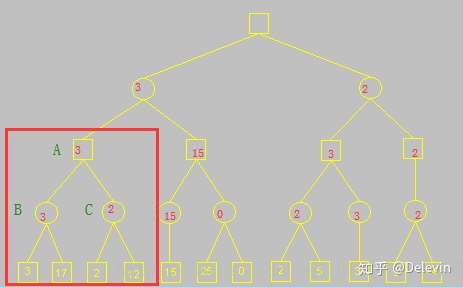
同理,计算其他节点,如下图:
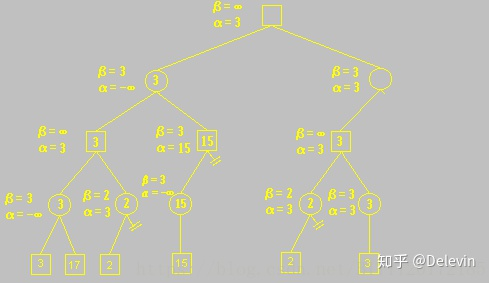
原文摘自 delevin