论文原地址:https://arxiv.org/pdf/1512.00727.pdf

一、介绍
缓存是计算机科学中提高系统性能的最基本、最有效的方法之一。它是通过将一小部分数据项保存在更快和/或更接近应用程序的内存中来获得的,这些内存的设置使得整个数据域无法装入这个快速附近的内存中。缓存能够工作的直观原因是,在计算机科学的许多领域中,数据访问显示出相当程度的局部性。捕捉本地更正式的方法是描述所有可能的数据项的访问频率通过一个概率分布,并指出在许多有趣的计算机科学领域,概率分布是高度倾斜,这意味着少量的对象更可能比其他对象访问。此外,在许多工作负载中,访问模式以及相应的概率分布会随时间变化。这种现象也被称为时间局部性。
当一个数据项被访问时,如果它已经出现在缓存中,我们说有一个缓存命中;缓存命中的次数和数据访问的总次数之间的比率被称为缓存命中比率。因此,如果保存在缓存中的项对应于访问最频繁的项,那么缓存很可能产生较高的命中率。
由于缓存大小通常是有限的,缓存设计者面临着如何选择存储在缓存中的项的困境。特别是,当为缓存保留的内存满时,决定应该从缓存中驱逐哪些项。显然,驱逐决策应该以有效的方式进行,以避免出现回答这些问题所需的计算和空间开销超过使用缓存所带来的好处的情况。缓存机制用来决定哪些项和哪些项应该插入缓存的空间。
当数据访问模式的概率分布随时间不变时,很容易看出使用频率最低(LFU)的缓存命中率最高。根据 LFU,在一个大小为 n 个条目的缓存中,在每个时刻,到目前为止的 n 个最经常使用的条目被保存在缓存中。然而,LFU 有两个明显的局限性。首先,已知的 LFU 实现需要维护大而复杂的元数据。其次,在大多数实际工作负载中,访问频率会随着时间发生根本变化。例如,考虑一个视频缓存服务,某天非常流行的视频片段可能几天后就不会被访问了。因此,一旦该项的流行度消退,仅仅因为它曾经非常流行就将其保留在缓存中是没有意义的。
让我们注意到,由于为所有遇到的对象维护频率直方图的成本太高,已经发布的实现 LFU 方案的作品只维护当前存在于缓存中条目的频率直方图的写、读和时间。因此,我们通过将前者(维护全量的缓存访问频率)称为完美的 LFU (PLFU) 而将后者(只维护当前在内存中的缓存的读写频率)称为内存中的LFU来区分它们。由于 WLFU 优于内存中的 LFU8[2],这里我们只处理 WLFU 和 PLFU。
LFU 的一个流行的替代方法依赖于时间局部性属性,这个替代方法称为“最近最少使用”(LRU),通过它,最后访问的项总是插入到缓存中,而最近最少访问的项则被驱逐(当缓存已满时)。与 LFU 相比,LRU 的实现效率更高,可以自动适应数据访问模式的时间变化和工作负载的激增。然而,在许多工作负载下,为了获得相同的命中率,LRU 需要比 LFU 大得多的缓存(因为无法保证缓存的命中率,低命中率的缓存也会在内存中存放较长时间)。同时对于硬件缓存和操作系统页面缓存来说,LRU 仍然被认为太慢,因此在这些高要求的情况下,我们发现使用 LRU 的近似实现比精确的 LRU 实现效果更好。
二、前置算法介绍
LRU
LRU(Least recently used,最近最少使用)算法根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高”。
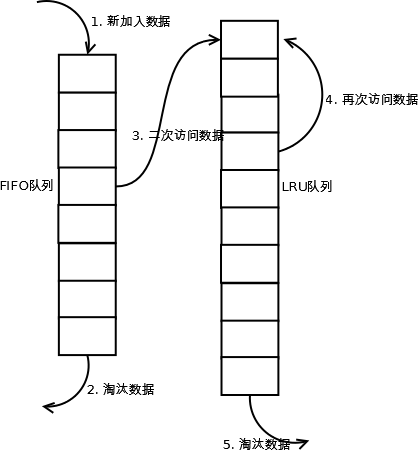
- 新数据插入到链表头部;
- 每当缓存命中(即缓存数据被访问),则将数据移到链表头部;
- 当链表满的时候,将链表尾部的数据丢弃。
过程如下:
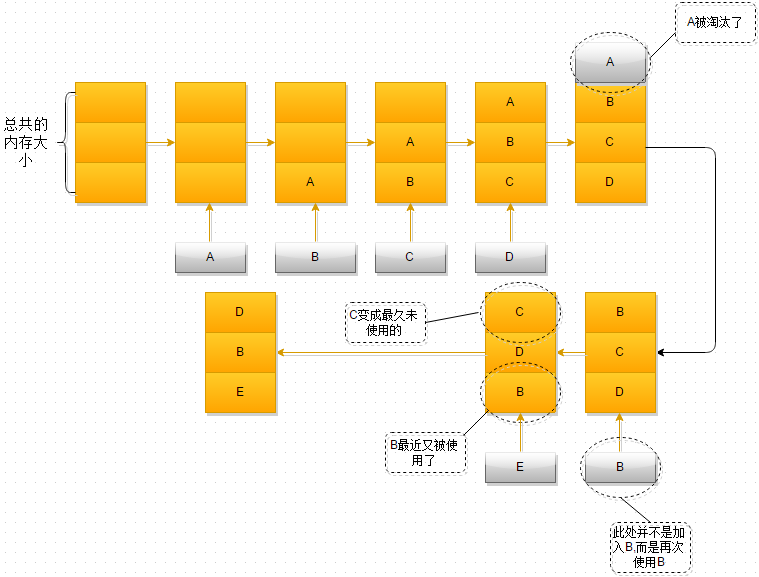
- 最开始时,内存空间是空的,因此依次进入A、B、C是没有问题的
- 当加入 D 时,就出现了问题,内存空间不够了,因此根据 LRU 算法,内存空间中 A 待的时间最为久远,选择A,将其淘汰
- 当再次引用 B 时,内存空间中的 B 又处于活跃状态,而 C 则变成了内存空间中,近段时间最久未使用的
- 当再次向内存空间加入 E 时,这时内存空间又不足了,选择在内存空间中待的最久的 C 将其淘汰出内存,这时的内存空间存放的对象就是 E->B->D。
我们知道链表的特性,读取时得按顺序读取,如果我们判断一个 key 在不在缓存中需要通过遍历整个列表,那我们把数组换成链表就没有意义了。要说拿到一个 key 就能判断它存不存在,就得说到哈希表,可以以 O(1) 的时间复杂度读取元素。如果我们用哈希表来记录链表中已经存在的节点,我们就可以快速判断当前这个 key 有没有数据被保存在链表中了。如果一个元素已经在链表中缓存了,那要把它提前到链表的头部 head 位置,我们还得把这个元素所在节点前后两个节点连接起来。对于单链表,找到它后面的节点很方便,要找到它前面的节点就得再次遍历链表了,这个时间复杂度太大了,所以我们使用一个额外的字段来记录它前一个节点,也就是 双链表。
我们可以用一个 HahsMap,一个双向链表来实现。
哈希表是由若干个 Key-Value 所组成。在“逻辑”上,这些 Key-Value 是无所谓排列顺序的,谁先谁后都一样。
HahsMap 用于快速查找到结点所在位置,然后将使用到的结点放在对头,这样最近最少使用的结点自然就落入到队尾。双向链表提供了良好的灵活性,两边可达。
LFU
LFU 的全称为 Least Frequently Used,意思就是最不频繁使用,所以 LFU 算法会淘汰掉使用频率最低的数据。如果存在相同使用频率的数据,则再根据使用时间间隔,将最久未使用的数据淘汰。
LFU将数据和数据的访问频次保存在一个容量有限的容器中,当访问一个数据时:
- 该数据在容器中,则将该数据的访问频次加 1。将该节点从原双向链表中移除,添加到新的访问次数对应的双向链表中。如果原来访问次数对应的双向链表在移除该节点之后,只剩下了 head 节点和 tail 节点,说明没有真实的业务数据节点存在,则需要从访问次数 hash 表中移除这个链表。
- 该数据不在容器中,则将该数据加入到容器中,且访问频次为 1。如果还未达到最大容量,则插入新的数据节点。节点的访问次数为1,如果hash表中不存在对应的双向链表则需要先创建链表;
- 当数据量达到容器的限制后,会剔除掉访问频次最低的数据。如果超过了最大容量,则需要先删除访问次数最低的节点,再插入新节点。节点的访问次数为 1,如果 hash 表中不存在 1 对应的双向链表则需要先创建链表。
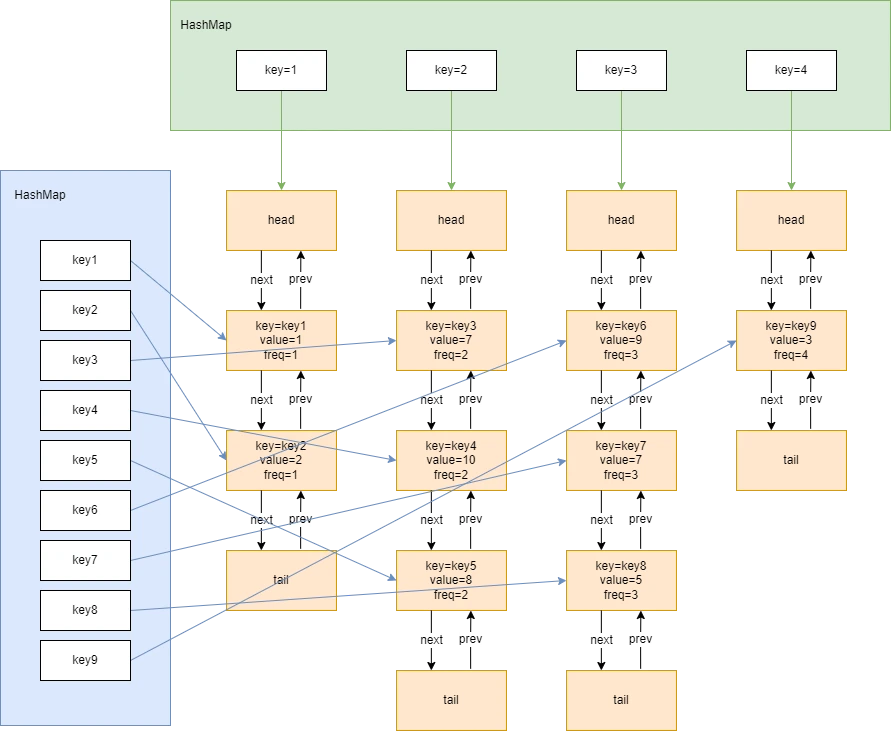
LFU 算法需要两个 hash 表+多个双向链表才能实现。
Bloom Filter

Bloom Filter 是 Burton Howard Bloom于1970年 提出,牺牲些许准确性,就换取了时空上的高效性,实在是很巧妙的设计。
Bloom Filter 底层使用一个位数组(bit array),初始,所表示集合为空时,所有位都为 0。
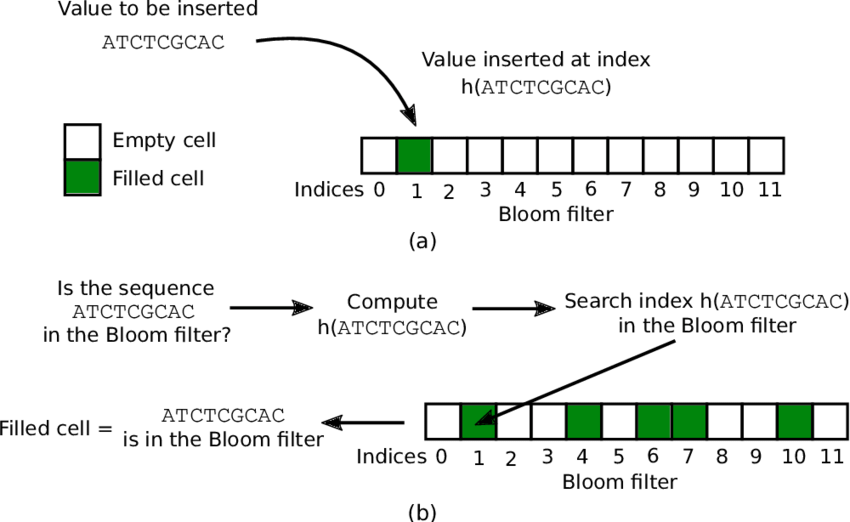
当往集合中插入一个元素 x 时,利用 k 个独立的哈希函数分别对 x 进行散列,然后将 k 个散列值按数组长度取余后分别将数组中对应位置置为 1。
查找过程和插入过程类似,也是利用同样的 k 个哈希函数对待查找元素按顺序进行哈希,得到 k 个位置。如果位数组中 k 个位置上的位均为 1,则该元素有可能存在;否则,若任意一位置上值为 0,则该值一定不存在。对于下图来说,x1 有可能存在,x2 一定不存在。
当持续插入一些元素后,数组中会有大量位置被置 1,可以想象,肯定会有一些位置冲突,造成误判。使用 k 个独立哈希函数可以部分解决这个问题。但如果对于某个值 y,k 个 hash(y) 计算出来的位置,都恰好被其他时候插入的几个元素值设置为 1,则会误判 y 在集合中。
相对于其他表示数据集的数据结构,如平衡二叉搜索树、Trie 树、哈希表,甚至更简单的数组或者链表,Bloom Filter 有着巨大的时空优势。上述提到的表示数据集的数据结构,大都需要对数据项本身存储,可能有的做了压缩,比如 Trie 树。但是 Bloom Filter 走了另一条路,并不存储数据项本身,而是存储数据项的几个哈希值,并且用高效紧凑的位数组来存,避免了指针的额外开销。
如此设计,使得 Bloom Filter 的大小与数据项本身大小(如字符串的长短)无关。如,具有 1% 的误差和最佳 k(哈希函数个数)的 Bloom Filter 来说,平均每个元素只需 9.6 bit。
CM-Sketch
论文地址:http://dimacs.rutgers.edu/~graham/pubs/papers/cm-full.pdf
Count-Min Sketch 是一种可以处理等值查询,Join 大小估计等的数据结构,并且可以提供很强的准确性保证。自 2003 年在文献 An improved data stream summary: The count-min sketch and its applications 中提出以来,由于其创建和使用的简单性获得了广泛的使用。 Count-Min Sketch 维护了一个 d*w 的计数数组,对于每一个值,用 d 个独立的 hash 函数映射到每一行的一列中,并对应修改这 d 个位置的计数值。如下图所示:
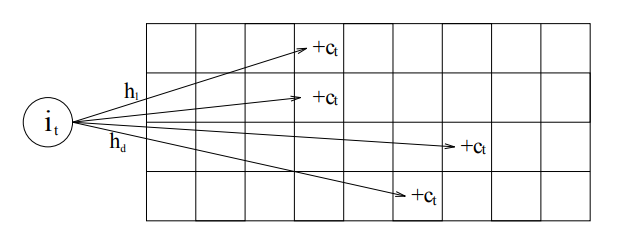
这样在查询一个值出现了多少次的时候,依旧用 d 个 hash 函数找到每一行中被映射到的位置,取这 d 个值的最小值作为估计值。

对于 Hash Function 的要求,可以是最简单的 hash function ,但所有的 hash function 必须不同.
- 添加元素
当一个新的类型 i 事件到达时,我们更新如下:对于表中的每一行 j,应用相应的散列函数来获得列索引 k = hj(i)。然后将第 j 行第 k 列中的值加 1。

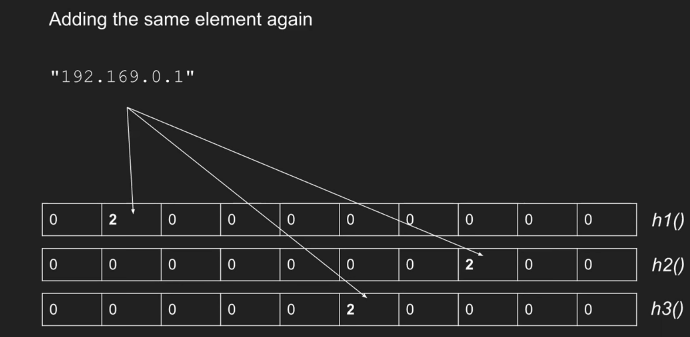
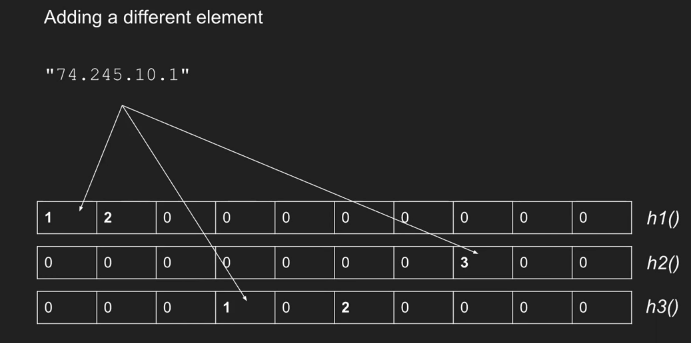
2.查询(统计元素个数)
取最小的 count 作为 element 出现的次数,故名 count-min。


三、TinyLFU 做了什么?
更好的保存访问频率
我们知道 LFU 中间的F代表的是 Frequency。但是保存每一个数据项的访问频率信息是不现实的,这样会带来巨大的开支。Tiny-LFU 使用的是 CM-Sketch,作为一个近似计算访问次数据结构。值得注意的是 CM-Sketch 记录的是访问次数,而不是频率,而且从访问次数中是代表不了频率信息的。
在合适的条件下将原有的统计信息减半,将这些信息代表频率信息。显然在这个算法中,我们并不关心频率具体是多少,在意的是访问频率谁高谁低,这个方法就能很好的解决这个问题。论文附带了论证过程。
更好的减少内存
分两个不分,一个是 Counters 本身更小,其次是是只需要更少的 counters 。正如前文所说,由于统计信息会在合适的时机减半,此外也只关注大小的信息不关心具体的数据,使用 counter 就可以使用很少的 bit。
Doorkeeper 是 approximate counting scheme 前面的一个 bloom filter,一个元素添加的时候,如果不在这个里面,则先添加到 Doorkeeper 里面,如果存在,则直接添加到主结构里面。每次访问元素时,如果在 Doorkeepe r里面,那么就是主结构里面的数值加上1,如果不存在就只使用主结构里面的数据。这么做的原因是可以减少主结构的大小。每一次 reset 操作会清空 Doorkeeper。
改进后的 W-TinyLFU
W-TinyLFU 近似在 Tiny-LFU 前面添加了小的 LRU,大约只占 1% 的数据。用来解决突发的稀疏流量。
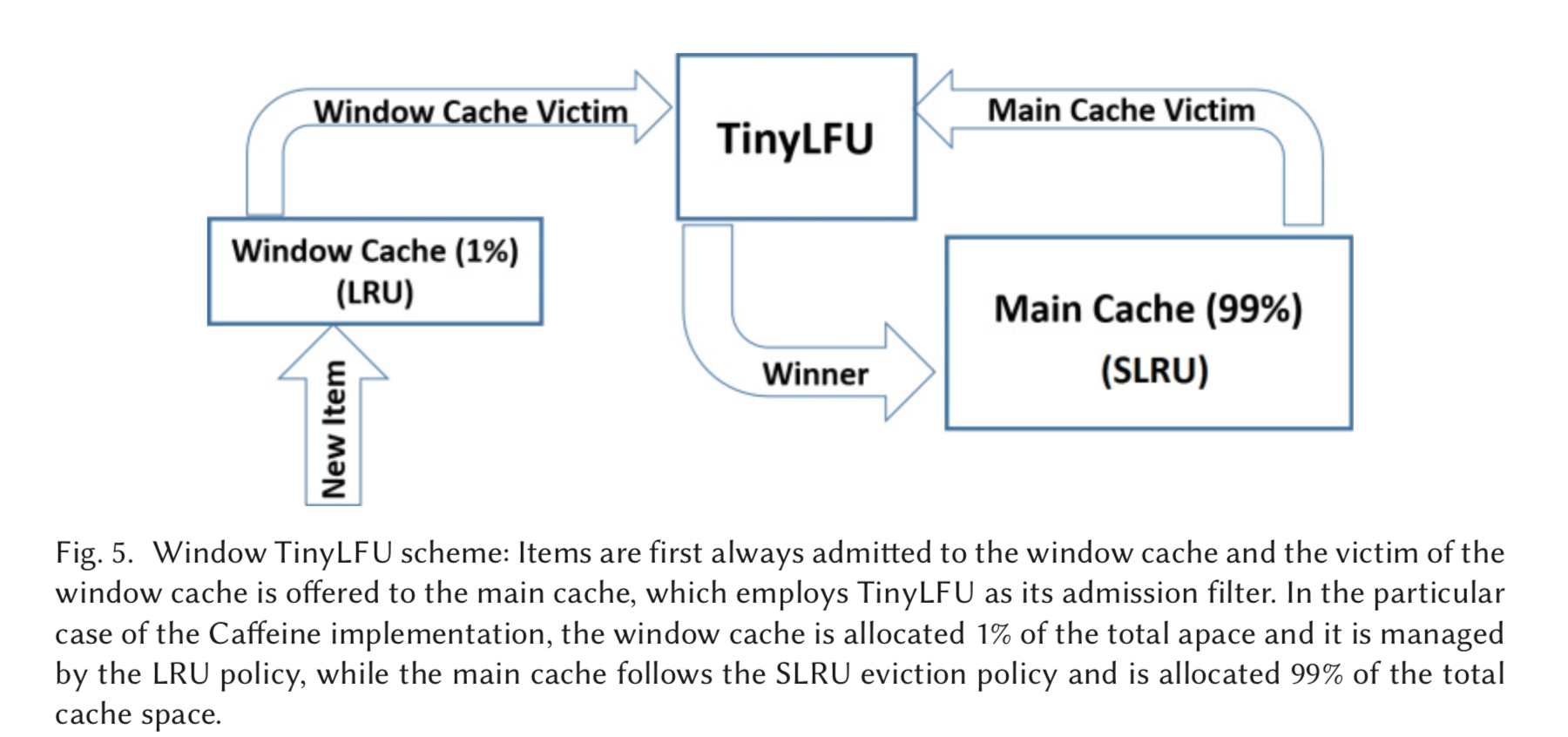
一般基于频率的 cache management policy 都存在这个问题:一个突发的频繁访问少量的对象,大部分的范围都集中,这样就会是其它的数据项的频率估计出现较大的误差。这里使用的方法就是在前面加一个小的 LRU,挡住这些频繁被访问的项来解决这个问题。 对于main cache ,使用之前存在的算法, 这里使用的是 SLRU。
四、TinyLFU 设计

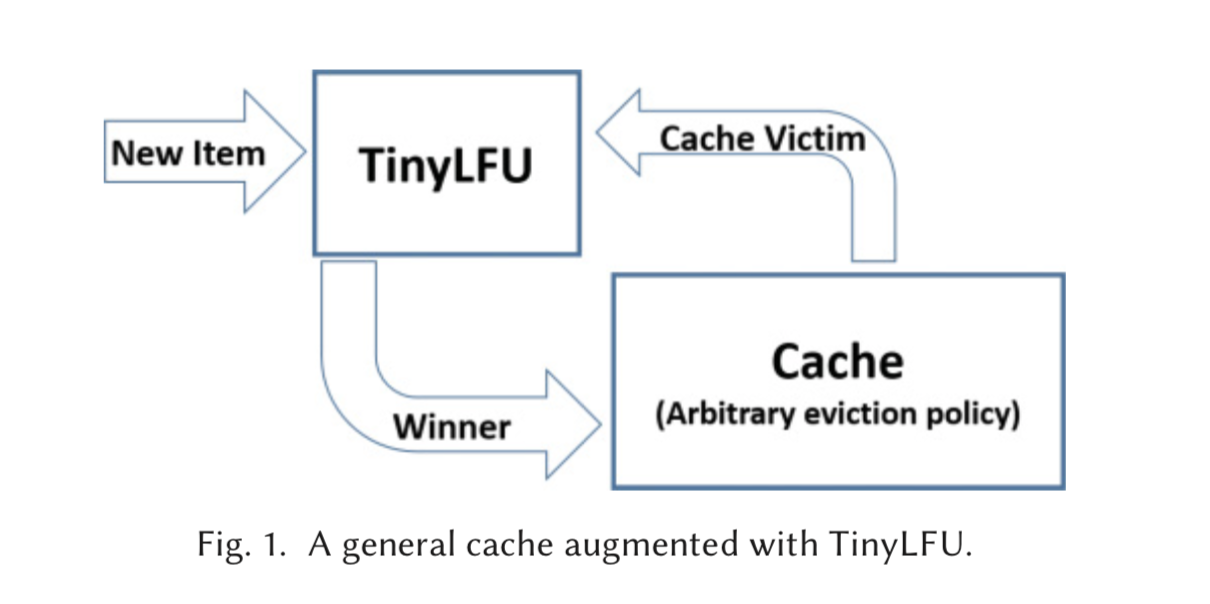
TinyLFU 的架构如上图所示。在这里,缓存清除策略选择一个缓存驱逐对象,而 TinyLFU 决定是否用新项替换缓存驱逐对象以增加命中率。
为此,TinyLFU维护了一个相当大的近期历史上项目频率的统计数据。对于实际实现来说,存储这些统计数据被认为是非常昂贵的,因此 TinyLFU 以一种高效的方式逼近它们。在下面,我们将描述 TinyLFU 所使用的技术,其中一些是对已知的近似计算技术的修改,而另一些则是特别为缓存上下文而创建的新方法。
近似计算
TinyLFU 是一种为了解决传统 LFU 算法空间存储比较大的问题 LFU 算法,它可以在较大访问量的场景下近似的替代 LFU 的数据统计部分,它的原理有些类似 BloomFilter 。首先回顾一下 BloomFilter 原理:在 BloomFilter 中,使用一个大的 bit 数组用于存储所有 key,每一个 key 通过多次不同的 hash 计算来映射数组的不同 bit 位,如果 key 存在将对应的 bit 位设置为 1,这样就可以通过少量的存储空间进行大量的数据过滤。在 TinyLFU 中,把多个 bit 位看做一个整体,用于统计一个 key 的使用频率,TinyFLU 中的 key 也是通过多次不同的 hash 计算来映射多个不同的 bit 组。在读取时,取映射的所有值中的最小的值作为 key 的使用频率。
在 Caffeine 中,维护了一个 4-bit CountMinSketch 用来记录 key 的使用频率。4-bit 也就意味着,统计的 key 最大使用频率为 15,具体的实现逻辑可以参考源代码中的 FrequencySketch 类。每个 entry 使用 8 bytes 以保证准确。
更新机制
为了解决数据访问模式随时间变化的问题,也为了避免计数无限增长,TinyLFU 还采用了一种基于滑动窗口的时间衰减设计机制,借助于一种简易的 reset 操作:每次添加一条记录到 Sketch 的时候,都会给一个计数器上加 1,当计数器达到一个尺寸 W 的时候,把所有记录的 Sketch 数值都除以 2,该 reset 操作可以起到衰减的作用。
由于我们的重置操作使用整数除法,它引入了截断错误。也就是说,在复位操作之后,计数器的值可能比浮点计数器的值低 0.5。如果我们必须再次复位,在复位之后,前一个复位操作的截断误差除以 0.25,但是我们积累了一个新的截断误差 0.5,导致总误差为 0.75。很容易看出,最坏情况下截断误差最多收敛到比项的准确率低一点。因此,截断错误对一个项目的记录发生率的影响在复位操作后高达 2/w。这意味着样本容量越大,截断误差越小。
更新机制衰减数学证明

主要问题及解决方案
一、长尾流量
Caffeine在TinyLFU之前加一个Dookeeper(BloomFilter),过滤这种低频数据:
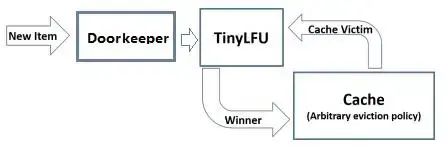
如果一个元素,在 Doorkeeper 中,则直接插入 TinyLFU 的主结构,否则先插入 Doorkeeper 。对于数据查询,会将 Doorkeeper 中的那一个计数值也加到计数值上去。这样 DoorKeeper 就可以将低频数据拦截住,降低了计数器数量。
二、时间变化影响的频率
如果整体计数超过某个阈值,会对 TinyLFU 所有的统计计数进行衰减。保障剔除历史频率很高但之后不经常使用的数据,另外也降低了内存消耗。
三、突发性的稀疏访问
Caffeine 采用了 Window TinyLFU 机制来解决这个问题:
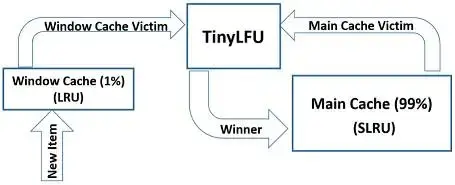
增加一个只占总体缓存 1% 大小的 Window 缓存(内部采用 LRU 算法),所有的新数据都先进入 Window 缓存。当 Window 缓存满了,淘汰的数据进入 TinyLFU 流程,这个被称为 W-TinyLFU 算法,它保证了突发的数据有机会被保留下来。另外 W-TinyLFU 的 Main Cache 淘汰算法采用了分段 LRU 算法,进而保障突发热数据有机会被保留下来。W-TinyLFU 算法已经被证明可以适应时间变化进而提供近似最佳的命中率。
主缓存根据 SLRU 策略静态划分为 A1 和 A2 两个区域,80% 的空间分配给热门项目(A2),并从 20% 的非热门项目(A1)中挑选 victim。所有请求的 key 都会被允许进入 window cache,而 window cache 的 victim 则有机会被允许进入主缓存。如果被接受,则 W-TinyLFU 的 victim 是主缓存的 victim,否则是窗口缓存的 victim。
在 caffeine 所有的数据都在 ConcurrentHashMap 中,这个和 guava cache 不同, guava cache 是自己实现了个类似 ConcurrentHashMap 的结构。在 caffeine 中有三个记录引用的LRU队列:
- Eden 队列:在 caffeine 中规定只能为缓存容量的 %1,如果 size=100 ,那这个队列的有效大小就等于 1。这个队列中记录的是新到的数据,防止突发流量由于之前没有访问频率,而导致被淘汰。比如有一部新剧上线,在最开始其实是没有访问频率的,防止上线之后被其他缓存淘汰出去,而加入这个区域是最舒服最安逸的区域,在这里很难被其他数据淘汰。
- Probation 队列:在这个队列就代表你的数据相对比较冷,马上就要被淘汰了。有效大小为 size - eden - protected。
- Protected 队列:在这个队列中,可以稍微放心一下了,你暂时不会被淘汰,但是别急,如果 Probation 队列没有数据了或者 Protected 数据满了,你也将会被面临淘汰的尴尬局面。当然想要变成这个队列,需要把 Probation 访问一次之后,就会提升为 Protected 队列。这个有效大小为( size - eden) x 80% 如果 size =100,就会是79。
这三个队列关系如下:
- 所有的新数据都会进入 Eden。
- Eden 满了,淘汰进入 Probation。
- 如果在 Probation 中访问了其中某个数据,则这个数据升级为 Protected。
- 如果 Protected 满了又会继续降级为 Probation。
对于发生数据淘汰的时候,会从 Probation 中进行淘汰。会把这个队列中的数据队头称为受害者,这个队头肯定是最早进入的,按照 LRU 队列的算法的话那他其实他就应该被淘汰,但是在这里只能叫他受害者,这个队列是缓刑队列,代表马上要给他行刑了。这里会取出队尾叫候选者,也叫攻击者。这里受害者会和攻击者PK决出我们应该被淘汰的。
通过我们的 Count-Min Sketch 中的记录的频率数据有以下几个判断:
- 如果攻击者大于受害者,那么受害者就直接被淘汰。
- 如果攻击者 <=5,那么直接淘汰攻击者。这个逻辑在他的注释中有解释:
他认为设置一个预热的门槛会让整体命中率更高。 - 其他情况,随机淘汰。